Quantum mechanics

[ New messages · Members · Forum rules · Search · RSS ]

Page 1 of 1
1

Forum » Concept of Physics » Concept of Physics » Quantum mechanics (Quantum mechanics Example)

Quantum mechanics

pradeep

Date: Monday, 03 October 11, 3:46 PM | Message # 1

Group: Administrators

Messages: 82

Status: Offline

Free particle

For example, consider a free particle. In quantum mechanics, there is wave-particle duality so the properties of the particle can be described as the properties of a wave. Therefore, its quantum state can be represented as a wave of arbitrary shape and extending over space as a wave function. The position and momentum of the particle are observables. The Uncertainty Principle states that both the position and the momentum cannot simultaneously be measured with full precision at the same time. However, one can measure the position alone of a moving free particle creating an eigenstate of position with a wavefunction that is very large (a Dirac delta) at a particular position x and zero everywhere else. If one performs a position measurement on such a wavefunction, the result x will be obtained with 100% probability (full certainty). This is called an eigenstate of position (mathematically more precise: a generalized position eigenstate (eigendistribution)). If the particle is in an eigenstate of position then its momentum is completely unknown. On the other hand, if the particle is in an eigenstate of momentum then its position is completely unknown.^[48] In an eigenstate of momentum having a plane wave form, it can be shown that the wavelength is equal to h/p, where h is Planck's constant and p is the momentum of the eigenstate.^[49]

3D confined electron wave functions for each eigenstate in a Quantum Dot. Here, rectangular and triangular-shaped quantum dots are shown. Energy states in rectangular dots are more ‘s-type’ and ‘p-type’. However, in a triangular dot the wave functions are mixed due to confinement symmetry.

Step potential

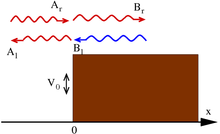
Main article: Solution of Schrödinger equation for a step potential

The step potential with incident and exiting waves shown.

The potential in this case is given by:

$V(x)= \begin{cases} 0, & x < 0, \\ V_0, & x \ge 0. \end{cases}$

The solutions are superpositions of left and right moving waves:

$\psi_L(x)= \frac{1}{\sqrt{k_0}} \left(A_r e^{i k_0 x} + A_l e^{-ik_0x}\right)\quad x<0$ ,

$\psi_R(x)= \frac{1}{\sqrt{k_1}} \left(B_r e^{i k_1 x} + B_l e^{-ik_1x}\right)\quad x>0$

where the wave vectors are related to the energy via

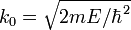$k_0=\sqrt{2m E/\hbar^2}$ , and

$k_1=\sqrt{2m (E-V_0)/\hbar^2}$

and the coefficients A and B are determined from the boundary conditions and by imposing a continuous derivative to the solution.

Each term of the solution can be interpreted as an incident, reflected of transmitted component of the wave, allowing the calculation of transmission and reflection coefficients. In contrast to classical mechanics, incident particles with energies higher than the size of the potential step are still partially reflected.

Rectangular potential barrier

Main article: Rectangular potential barrier

This is a model for the quantum tunneling effect, which has important applications to modern devices such as flash memory and the scanning tunneling microscope.

Particle in a box

1-dimensional potential energy box (or infinite potential well)

Main article: Particle in a box

The particle in a 1-dimensional potential energy box is the most simple example where restraints lead to the quantization of energy levels. The box is defined as having zero potential energy inside a certain region and infinite potential energy everywhere outside that region. For the 1-dimensional case in the $x$ direction, the time-independent Schrödinger equation can be written as:^[50]

$- \frac {\hbar ^2}{2m} \frac {d ^2 \psi}{dx^2} = E \psi.$

Writing the differential operator

$\hat{p}_x = -i\hbar\frac{d}{dx}$

the previous equation can be seen to be evocative of the classic analogue

$\frac{1}{2m} \hat{p}_x^2 = E$

with $E$ as the energy for the state $ψ$ , in this case coinciding with the kinetic energy of the particle.

The general solutions of the Schrödinger equation for the particle in a box are:

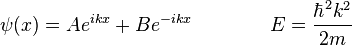
$\psi(x) = A e^{ikx} + B e ^{-ikx} \qquad\qquad E = \frac{\hbar^2 k^2}{2m}$

or, from Euler's formula,

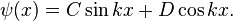
$\psi(x) = C \sin kx + D \cos kx.\!$

The presence of the walls of the box determines the values of C, D, and k. At each wall (x = 0 and x = L), ψ = 0. Thus when x = 0,

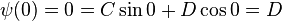
$\psi(0) = 0 = C\sin 0 + D\cos 0 = D\!$

and so D = 0. When x = L,

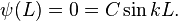
$\psi(L) = 0 = C\sin kL.\!$

C cannot be zero, since this would conflict with the Born interpretation. Therefore sin kL = 0, and so it must be that kL is an integer multiple of π. Therefore,

$k = \frac{n\pi}{L}\qquad\qquad n=1,2,3,\ldots.$

The quantization of energy levels follows from this constraint on k, since

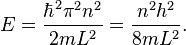
$E = \frac{\hbar^2 \pi^2 n^2}{2mL^2} = \frac{n^2h^2}{8mL^2}.$

Finite potential well

Main article: Finite potential well

This is generalization of the infinite potential well problem to potential wells of finite depth.

Harmonic oscillator

Main article: Quantum harmonic oscillator

As in the classical case, the potential for the quantum harmonic oscillator is given by:

$V(x)=\frac{1}{2}m\omega^2x^2$

This problem can be solved either by solving the Schrödinger equation directly, which is not trivial, or by using the more elegant ladder method, first proposed by Paul Dirac. The eigenstates are given by:

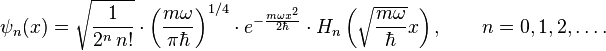
$\psi_n(x) = \sqrt{\frac{1}{2^n\,n!}} \cdot \left(\frac{m\omega}{\pi \hbar}\right)^{1/4} \cdot e^{ <br /> - \frac{m\omega x^2}{2 \hbar}} \cdot H_n\left(\sqrt{\frac{m\omega}{\hbar}} x \right), \qquad n = 0,1,2,\ldots.$